在过去几十年里,随着数据收集与处理能力的显著提高,各行各业都在面对由海量高维数据带来的机遇与挑战。然而,在处理这些高维数据时,传统的数据分析方法往往过分依赖于特征间的线性相关性。尽管这些线性方法能够简化数据的表示形式,但它们在捕捉数据中的复杂模式方面却显得力不从心。一个典型的例子是,高维数据往往聚集在低维流形附近,而这些特征无法有效地通过低维线性结构来表达。
针对这一问题,流形学习技术成为一种具有前景的解决方案。然而,现有的流形学习方法,如基于流形结构的嵌入和去噪算法,因缺乏深入的几何理解和坚实的理论基础而受到限制。此外,在处理极大规模数据集时,这些技术常面临着计算效率和精度的双重挑战,特别是在生物信息学、金融分析和社会网络数据等应用领域中。
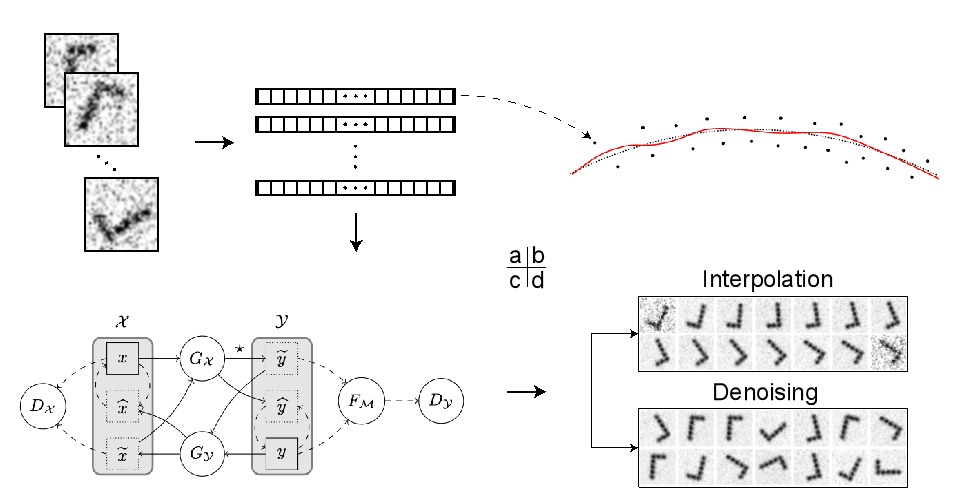
为了深入研究高维数据中的非线性结构,新加坡国立大学统计与数据科学系的研究团队和清华丘成桐数学中心团队提出了一种新算法。该算法基于数据统计分布和隐含几何结构,旨在从高维环境空间中的离散样本点恢复出光滑的低维流形结构。研究人员将高维空间中的观测样本视为未知流形的隐藏信息与环境噪声的混合体。他们通过利用数据中的几何平滑特征及统计收敛性质,估计样本点到流形的距离,并据此给出未知流形的估计及样本点到其上的投影。这种对流形的估计被证明具有给定维数的光滑流形特性,且其估计误差和收敛速度均优于现有方法。此外,为了应对数据维度和数据量的计算挑战,研究人员将此方法与深层生成对抗网络(GANs)结合(如图1(c) 所示),通过循环生成对抗网络学习高低维空间之间的连续映射,来估计隐藏流形的指对数映射,并利用这些映射实现对隐藏流形的初步估计。团队已将该方法应用于欧式空间中的几何模型、卡拉比-丘流形,以及一系列图像数据(图1 (a, d)),并正在尝试处理分析更高维度的前沿实验数据,例如单细胞RNA序列数据。这项工作预计将极大地改变我们处理高维复杂数据集域的效率,并提供潜在的新的视角。
研究论文:Yao, Z., Su, J., & Yau, S. T. (2024). Manifold fitting with CycleGAN. Proceedings of the National Academy of Sciences, 121(5), e2311436121.https://doi.org/10.1073/pnas.2311436121
原创文章,如若转载,请注明出处。
